Damped Oscillations, Forced Oscillations and Resonance

Damped Oscillations, Forced Oscillations and Resonance

Damping in an Oscillating System

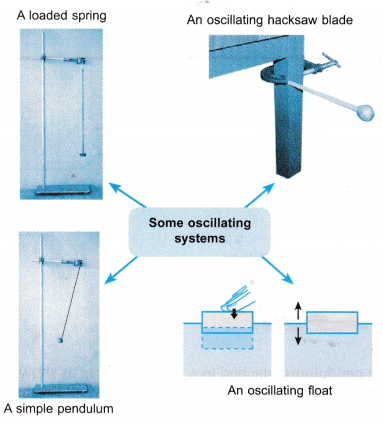
1. Figure shows some oscillating systems. Each oscillating system will oscillate with a smaller and smaller amplitude and eventually stop completely
2. This is due to energy loss from the oscillating systems resulting from factors like air resistance and friction in various parts of the systems.
3. Damping is said to have occurred in an oscillating system when the system loses energy to the surroundings, usually in the form of heat energy. The forces responsible for damping are often called dissipative forces because they dissipate the system’s energy.
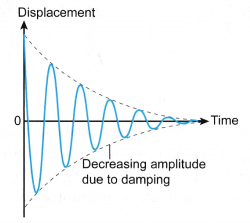
4. Figure shows the displacement-time graph of an oscillating system undergoing damping. The dotted lines indicate the decreasing of the amplitude of oscillation with time.
   

Forced Oscillations and Resonance

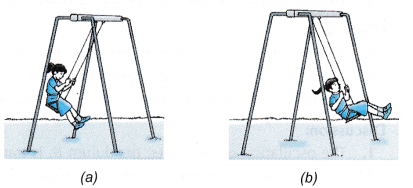
1. Figure shows a girl swinging on a swing. Damping occurs and the swing will oscillate with a smaller and smaller amplitude and eventually stop completely.
   
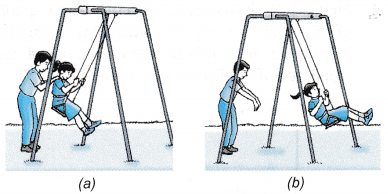
2. Figure shows a boy pushing a girl, who is swinging, each time when the swing reaches the highest position. By doing so, the swing will be able to oscillate continuously with a large amplitude.
   
3. A system oscillates at its natural frequency when no external force is applied on it. As an example, a simple pendulum has a natural frequency depending on its length. A longer pendulum has a lower frequency.
4. When a periodic force is applied to an oscillating system, the response depends on the frequency of the periodic force.
5. An oscillating system is said to be at resonance when it is driven at its natural frequency by a periodic force. Maximum energy transfer to the system occurs and it oscillates at a large amplitude.

Effects and Applications of Resonance

1. When steel was first used for making car bodies, there was the problem of a drumming sound at a certain speed of the cars. This was caused by resonance between the body panelling and the vibrations of the engine. The problem was solved by coating the inside of the panels with a layer of plastic material to damp out the vibrations.
   
2. Marching soldiers can damage the bridge they cross. This happens when their rate of marching matches the natural frequency of the oscillation of the bridge. Resonance occurs and the bridge oscillates with a large amplitude. It is advisable for soldiers to break step when crossing a bridge.
   
3. Wind instruments like saxophones, trumpets, flutes and clarinets make use of the effect of resonance of air to produce sound. The air blown into a wind instrument causes resonance of the air column inside the instrument, and thus a loud sound is produced by the instrument.
   
4. A radio receiver can be tuned to the same frequency as the incoming radio waves, transmitted from a broadcasting station, to set it into resonance so that a large current is induced. The induced current is amplified and converted into sound.

Resonance in an Oscillating System Experiment

Aim: To study resonance in an oscillating system.
Materials: String, thread
Apparatus: Retort stand, pendulum bobs, weights
Method:

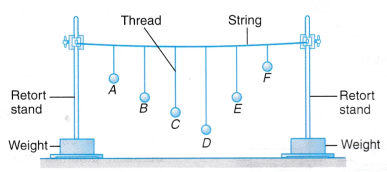
1. A Barton’s pendulum, which consists of a series of simple pendulums attached to a string, is set up as shown in Figure.
2. Pendulums B and E are of the same length. All the other pendulums are of different lengths. Pendulum B is pulled aside and released to set it into oscillation.
3. The oscillations of the other pendulums are observed.

Observations:

1. When pendulum B oscillates, the other pendulums also start to oscillate.
2. Pendulum E oscillates with maximum amplitude.
3. The other pendulums oscillate with very small amplitudes.

Discussion:

1. The oscillation of the driver, pendulum B, is transmitted along the supporting string.
2. The other pendulums are subjected to a periodic force from B. They start to oscillate.
3. Pendulums B and E have the same natural frequency because both are of the same length. Pendulum E received a bigger amount of energy from pendulum B compared to each of the other pendulums.

Conclusions:

1. Pendulum E is made to oscillate with maximum amplitude when energy is fed at its own natural frequency.
2. Resonance occurs when the natural frequency of a system corresponds to the frequency of the energy supplied.

The post Damped Oscillations, Forced Oscillations and Resonance appeared first on A Plus Topper.

from A Plus Topper
via Learning Made Simple 360

*Note that these contents are Autoblogged from A Plus Topper and cannot be edited.