Complex Numbers
Complex Numbers
“Complex number is the combination of real and imaginary numbers”
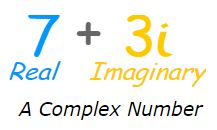
Basic concepts of complex number
Definition: A number of the form x + iy where x, y ϵ R and i = √-1 is called a complex number and ‘i’ is called iota.
A complex number is usually denoted by z and the set of complex number is denoted by C.
i.e., C = {x + iy : x ϵ R, y ϵ R, i = √-1}
For example, 5 + 3i, –1 + i, 0 + 4i, 4 + 0i etc. are complex numbers.
(i) Euler was the first mathematician to introduce the symbol i (iota) for the square root of – 1 with property i2 = –1. He also called this symbol as the imaginary unit.
(ii) For any positive real number a, we have
![]()
(iii) The property \(\sqrt { a } \sqrt { b } =-\sqrt { ab }\) is valid only if at least one of a and b is non-negative. If a and b are both negative then \(\sqrt { a } \sqrt { b } =-\sqrt { \left| a \right| \left| b \right| }\).
(2) Integral powers of iota (i) : Since hence we have i = √-1, i2 = –1, i3 = –i and i4 = 1. To find the value of in (n>4) first divide n by 4. Let q be the quotient and r be the remainder.
i.e., n = 4q + r where 0≤r≤3
in = i4q+r = (i4)q.(i)r = (1)q.(i)r
In general we have the following results i4n = 1, i4n+1 = i, i4n+2 = -1, i4n+3 = -i , where n is any integer.
Real and Imaginary parts of a complex number
If x and y are two real numbers, then a number of the form is called a complex number. Here ‘x’ is called the real part of z and ‘y’ is known as the imaginary part of z. The real part of z is denoted by Re(z) and the imaginary part by Im(z).
If z = 3 – 4i, then Re(z) = 3 and Im(z) = – 4.
A complex number z is purely real if its imaginary part is zero i.e., Im(z) = 0 and purely imaginary if its real part is zero i.e., Re(z) = 0.
Algebraic operations with complex numbers
Let two complex numbers be z1 = a + ib and z2 = c + id.
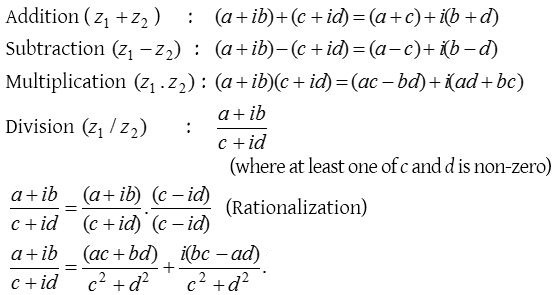
Properties of algebraic operations on complex numbers
Let z1, z2 and z3 are any three complex numbers then their algebraic operations satisfy following properties :
(i) Addition of complex numbers satisfies the commutative and associative properties
i.e., z1 + z2 = z2 + z1 and (z1 + z2) + z3 = z1 + (z2 + z3)
(ii) Multiplication of complex numbers satisfies the commutative and associative properties.
i.e., z1z2 = z2z1 and (z1z2)z3 = z1(z2z3)
(iii) Multiplication of complex numbers is distributive over addition
i.e., z1(z2 + z3) = z1z2 +z1z3 and (z2 + z3)z1 = z2z1 + z3z1
Equality of two complex numbers
Two complex numbers z1 = x1 + iy1 and z2 = x2 + iy2 are said to be equal if and only if their real and imaginary parts are separately equal.
i.e., z1 = z2 ⇔ x1 + iy1 = x2 + iy2 ⇔ x1 = x2 and y1 = y2.
Complex numbers do not possess the property of order i.e., (a+ib) < (or) > (c+id) is not defined. For example, the statement (9+6i) > (3+2i) makes no sense.
Conjugate of a complex number
(1) Conjugate complex number: If there exists a complex number z = a+ib, (a,b) ϵ R, then its conjugate is defined as \(\bar { z } =\quad a-ib\).
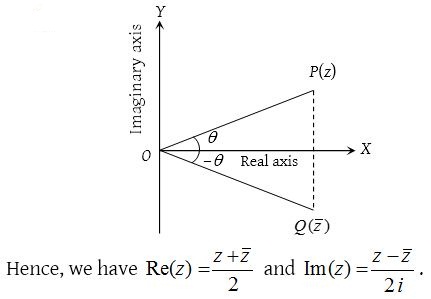
Geometrically, the conjugate of z is the reflection or point image of z in the real axis.
(2) Properties of conjugate: If z, z1 and z2 are existing complex numbers, then we have the following results:
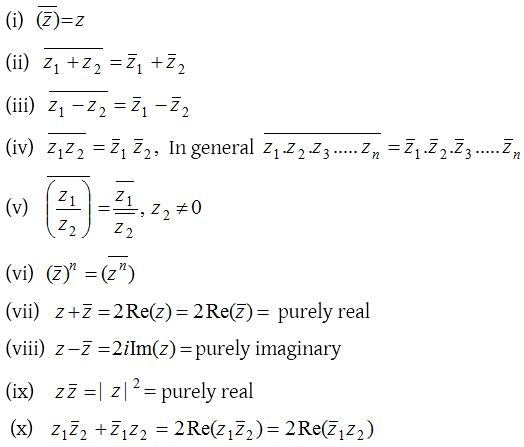
(3) Reciprocal of a complex number: For an existing non-zero complex number z = a+ib, the reciprocal is given by
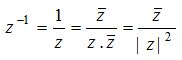
Modulus of a complex number
Modulus of a complex number z = a+ib is defined by a positive real number given by \(\left| z \right| =\sqrt { { a }^{ 2 }+{ b }^{ 2 } }\) where a, b real numbers. Geometrically |z| represents the distance of point P from the origin, i.e. |z| = OP.
If the corresponding complex number is known as unimodular complex number. Clearly z lies on a circle of unit radius having centre (0, 0).
Properties of modulus
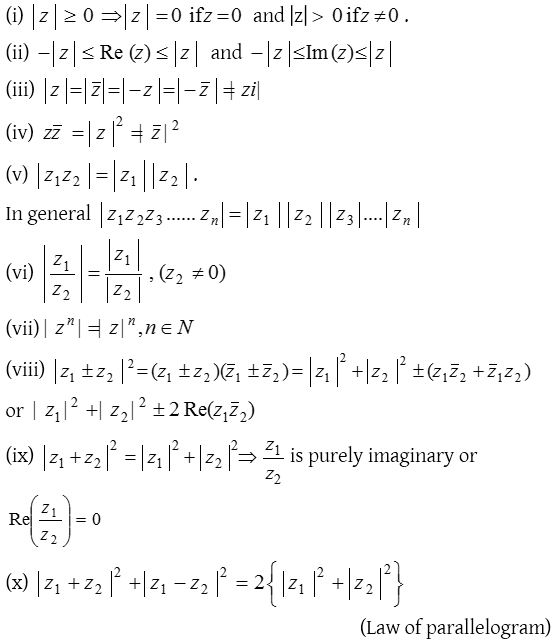
Square root of a complex number
Let z = a+ib be a complex number,
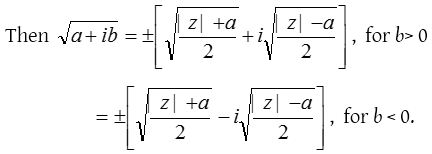
To find the square root of a–ib replace i by –i in the above results.
Various representations of a complex number
A complex number can be represented in the following form:
(1) Geometrical representation (Cartesian representation):
The complex number z = a+ib = (a, b) is represented by a point P whose coordinates are referred to rectangular axes XOX’ and YOY’ which are called real and imaginary axis respectively. This plane is called argand plane or argand diagram or complex plane or Gaussian plane.
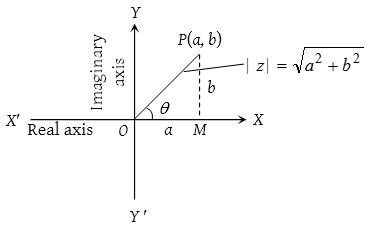
Distance of any complex number from the origin is called the modulus of complex number and is denoted by |z|, i.e., \(\left| z \right| =\sqrt { { a }^{ 2 }+{ b }^{ 2 } }\).
Angle of any complex number with positive direction of x–axis is called amplitude or argument of z.
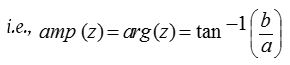
(2) Trigonometrical (Polar) representation:
In ∆ OPM, let OP = r, then a = r cos θ and b = r sin θ Hence z can be expressed as z = r(cos θ + i sin θ)
where r = |z| and θ = principal value of argument of z.
For general values of the argument
z = r[(cos(2nπ + θ) + i sin (2nπ + θ)]
Sometimes (cos θ + i sin θ) is written in short as cisθ.
(3) Vector representation:
If P is the point (a, b) on the argand plane corresponding to the complex number z = a+ib.
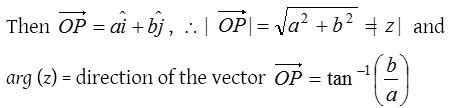
(4) Eulerian representation (Exponential form):
Since we have ei? = (cos θ + i sin θ) and thus z can be expressed as z = rei? , where |z|=r and arg (z).
The post Complex Numbers appeared first on A Plus Topper.
from A Plus Topper
via Learning Made Simple 360
*Note that these contents are Autoblogged from A Plus Topper and cannot be edited.
Join the conversation