How to Multiply Matrices

How to Multiply Matrices

Multiplication of matrices

Two matrices A and B are conformable for the product AB if the number of columns in A (pre-multiplier) is same as the number of rows in B (post multiplier). Thus, if A = [a_ij]_m×n  and B = [b_ij]_n×p are two matrices of order m × n and n × p respectively, then their product AB is of order and is defined as

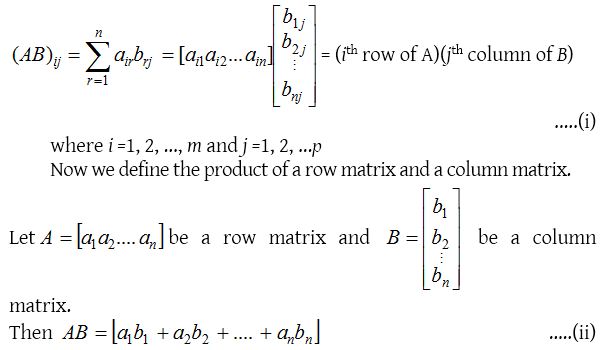
Thus, from (i), (AB)_ij = Sum of the product of elements of i^th row of A with the corresponding elements of j^th column of B.

Properties of matrix multiplication

If A,B and C are three matrices such that their product is defined, then

1. AB ≠ BA, (Generally not commutative)
2. (AB)C = A(BC), (Associative Law)
3. IA = A = AI, where I is identity matrix for matrix multiplication.
4. A(B + C) = AB + AC, (Distributive law)
5. If AB = AC ⇏ B = C, (Cancellation law is not applicable)
6. If AB = 0, it does not mean that A = 0 or B = 0, again product of two non zero matrix may be a zero matrix.

Scalar multiplication of matrices

Let A = [a_ij]_m×n be a matrix and k be a number, then the matrix which is obtained by multiplying every element of A by k is called scalar multiplication of A by k and it is denoted by kA.
Thus, if A = [a_ij]_m×n, then kA = Ak = [ka_ij]_m×n.

Properties of scalar multiplication:
If A, B are matrices of the same order and λ, μ are any two scalars then

1. λ (A + B) = λA + λB
2. (λ + μ)A = λ + μA
3. λ(μA) = (λμA) = μ(λA)
4. (-λA) = -(λA) = λ(-A)

All the laws of ordinary algebra hold for the addition or subtraction of matrices and their multiplication by scalars.

Multiplication of Matrices Problems with Solutions

1.

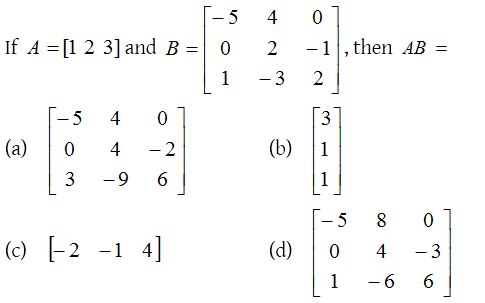
Solution:

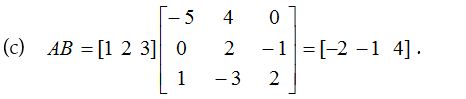
2.

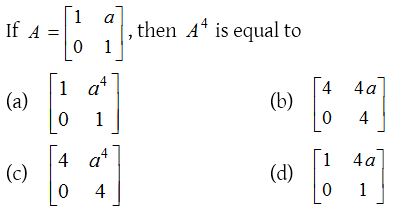
Solution:

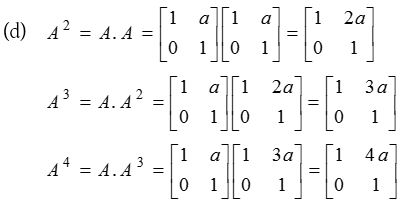
3.

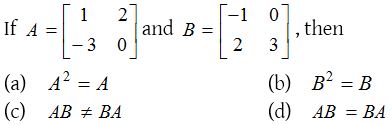
Solution:

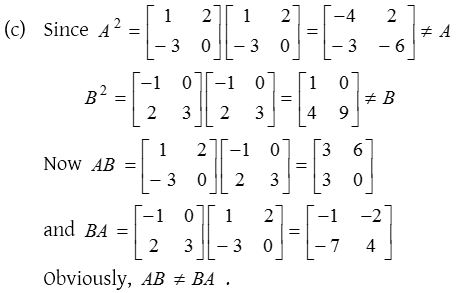
4.

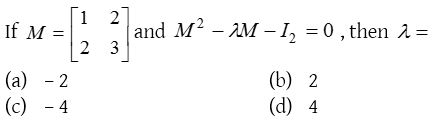
Solution:

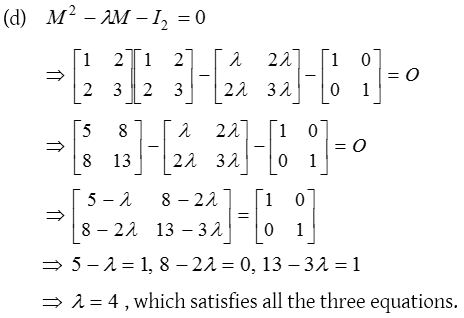
The post How to Multiply Matrices appeared first on A Plus Topper.

from A Plus Topper
via Learning Made Simple 360

*Note that these contents are Autoblogged from A Plus Topper and cannot be edited.