Multiplication and Division of Radicals

Multiplication and Division of Radicals

(For this lesson, the term “radical” will refer only to “square root”.)
When multiplying radicals, you must multiply the numbers OUTSIDE (O) the radicals AND then multiply the numbers INSIDE (I) the radicals.

When dividing radicals, you must divide the numbers OUTSIDE (O) the radicals AND then divide the numbers INSIDE (I) the radicals.

Should a radical appear in the denominator of a fraction, it will need to be “removed” if you are trying to simplify the expression.
To “remove” a radical from the denominator, multiply the top and bottom of the fraction by that same radical to create a rational number (a perfect square radical) in the denominator. This process is called rationalizing the denominator.

Example 1: Multiply √8 × √3
Multiply the values under the radicals.
√8 × √3 = √24
Then simplify the result.

Example 2: Multiply 5√5 × 3√10
Multiply out front and multiply under the radicals.
5√5 × 3√10 = 15√50
Then simplify the result.

Example 3: 

Multiply under the radicals.

Then simplify the result.

Example 4: Distribute √2(3√5 + √2)
Distribute across the parentheses. Remember there is an implied “1” in front of √2.

Then simplify the result.

Example 5: 

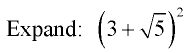
Use the distributive property to multiply. Combine like terms.

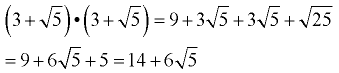
Example 6: Multiply (2 + √3) • (3 – √2)
Use the distributive property to multiply. There are NO like terms to be combined.
(2 + √3) • (3 – √2) = 6 – 2√2 + 3√3 – √6

Example 7:

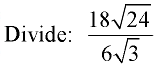
Divide out front and divide under the radicals.

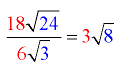
Then simplify the result.

Example 8:

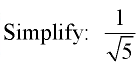
This fraction will be in simplified form when the radical is removed from the denominator. You need to create a perfect square under the square root radical in the denominator by multiplying the top and bottom of the fraction by the same value (this is actually multiplying by “1”). The easiest approach is to multiply by the square root radical you need to convert (in this case multiply by √5).

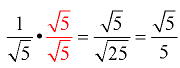
You have just “rationalized” the denominator!

The post Multiplication and Division of Radicals appeared first on A Plus Topper.

*Note that these contents are Autoblogged from A Plus Topper and cannot be edited.