Solving Linear Inequalities

Solving Linear Inequalities

Solving linear inequalities is the same as solving linear equations with one very important exception…

When you multiply or divide an inequality by a negative value, it changes the direction of the inequality.

Inequalities with one variable:

Consider:
Look at this true statement:
Suppose we multiply both sides by -1.
What is the relationship between these two numbers ?

ANS: -5 is less than -3 because it is further to the left on the number line.

So, we must change the direction of the inequality when we multiply (or divide) by a negative number in order to get the correct answer.

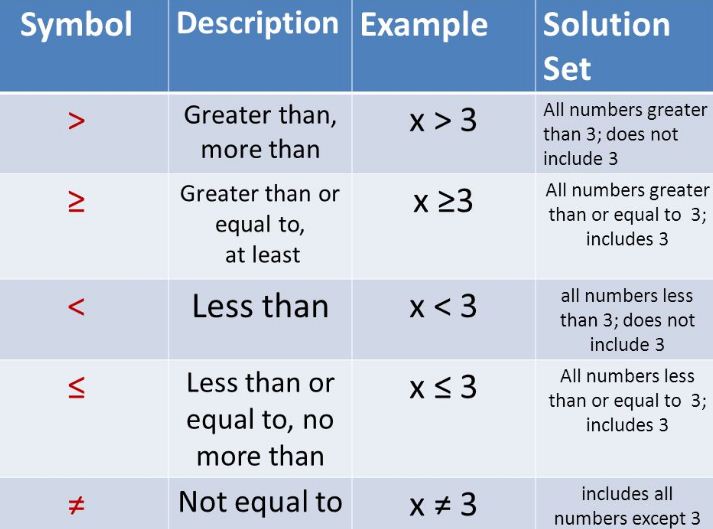
Before we begin our example problems, refresh your memory on what each inequality symbol means.
It is helpful to remember that the “open” part of the inequality symbol (the larger part) always faces the larger quantity.

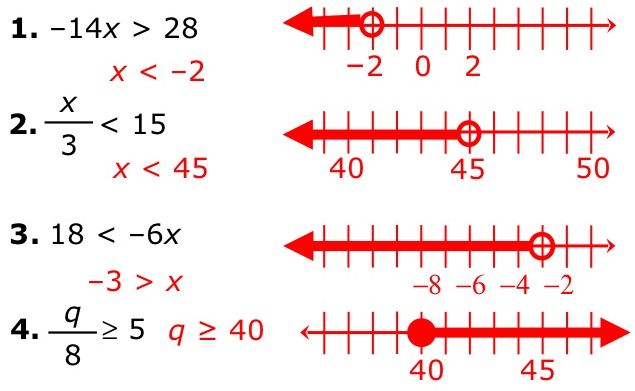
Example 1:

Example 2:

Example 3:

The post Solving Linear Inequalities appeared first on A Plus Topper.

from A Plus Topper
via Learning Made Simple 360

*Note that these contents are Autoblogged from A Plus Topper and cannot be edited.