What are Addition and Multiplication Theorems on Probability?

What are Addition and Multiplication Theorems on Probability?

Addition and Multiplication Theorem of Probability

State and prove addition and multiplication theorem of probability with examples

Equation Of Addition and Multiplication Theorem

Notations :

1. P(A + B) or P(A∪B) = Probability of happening of A or B
   = Probability of happening of the events A or B or both
   = Probability of occurrence of at least one event A or B
2. P(AB) or P(A∩B) = Probability of happening of events A and B together.

(1) When events are not mutually exclusive:
If A and B are two events which are not mutually exclusive, then
P(A∪B) = P(A) + P(B) – P(A∩B)
or P(A + B) = P(A) + P(B) – P(AB)
For any three events A, B, C
P(A∪B∪C) = P(A) + P(B) + P(C) – P(A∩B) – P(B∩C) – P(C∩A) + P(A∩B∩C)
or P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(BC) – P(CA) + P(ABC)

(2) When events are mutually exclusive:
If A and B are mutually exclusive events, then
n(A∩B) = 0 ⇒ P(A∩B) = 0
∴ P(A∪B) = P(A) + P(B).
For any three events A, B, C which are mutually exclusive,
P(A∩B) = P(B∩C) = P(C∩A) = P(A∩B∩C) = 0
∴ P(A∪B∪C) = P(A) + P(B) + P(C).
The probability of happening of any one of several mutually exclusive events is equal to the sum of their probabilities, i.e. if A₁, A₂ ……… A_n are mutually exclusive events, then
P(A₁ + A₂ + … + A_n) = P(A₁) + P(A₂) + …… + P(A_n)
i.e. P(Σ A_i) = Σ P(A_i).

(3) When events are independent :
If A and B are independent events, then P(A∩B) = P(A).P(B)
∴ P(A∪B) = P(A) + P(B) – P(A).P(B)

(4) Some other theorems

1.  Let A and B be two events associated with a random experiment, then
   
2. Generalization of the addition theorem :
   If A₁, A₂ ……… A_n are n events associated with a random experiment, then
   
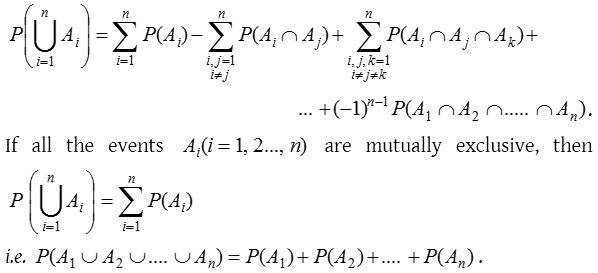
3. Booley’s inequality : If A₁, A₂ ……… A_n are n events associated with a random experiment, then
   
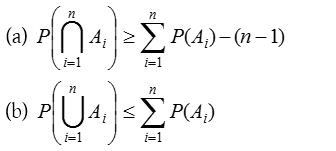
   These results can be easily established by using the Principle of mathematical induction.

Conditional probability

Let A and B be two events associated with a random experiment. Then, the probability of occurrence of A under the condition that B has already occurred and P(B) ≠ 0, is called the conditional probability and it is denoted by P(A/B).
Thus, P(A/B) = Probability of occurrence of A, given that B has already happened.

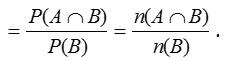
Similarly, P(B/A) = Probability of occurrence of B, given that A has already happened.

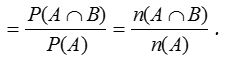
Sometimes, P(A/B) is also used to denote the probability of occurrence of A when B occurs. Similarly, P(B/A) is used to denote the probability of occurrence of B when A occurs.

Multiplication Theorem Of Probability

1. If A and B are two events associated with a random experiment, then P(A∩B) = P(A).P(B/A), if P(A) ≠ 0 or P(A∩B) = P(B).P(A/B), if P(B) ≠ 0.
2. Extension of multiplication theorem:
   If A₁, A₂ ……… A_n are n events related to a random experiment, then
   P(A₁∩A₂∩A₃∩ … ∩A_n) = P(A₁) P(A₂/A₁) P(A₃/A₁∩A₂)……P(A_n/A₁∩A₂∩…∩A_n−1),
   where P(A_i/A₁∩A₂∩…∩A_i−1), represents the conditional probability of the event , given that the events A₁, A₂ ……… A_i−1 have already happened.
3. Multiplication theorems for independent events:
   If A and B are independent events associated with a random experiment, then P(A∩B) = P(A).P(B) i.e., the probability of simultaneous occurrence of two independent events is equal to the product of their probabilities. By multiplication theorem, we have P(A∩B) = P(A).P(B/A). Since A and B are independent events, therefore P(B/A) = P(B). Hence, P(A∩B) = P(A).P(B).
4. Extension of multiplication theorem for independent events:
   If A₁, A₂ ……… A_n are independent events associated with a random experiment, then
   P(A₁∩A₂∩A₃∩ … ∩A_n) = P(A₁) P(A₂)..… P(A_n).
   By multiplication theorem, we have
   P(A₁∩A₂∩A₃∩ … ∩A_n) = P(A₁) P(A₂/A₁) P(A₃/A₁∩A₂)……P(A_n/A₁∩A₂∩…∩A_n−1)
   Since A₁, A₂ ………A_n-1, A_n are independent events, therefore
   P(A₂/A₁) = P(A₂), P(A₃/A₁∩A₂) = P(A₃),……, P(A_n/A₁∩A₂∩…∩A_n−1) = P(A_n)
   Hence, P(A₁∩A₂∩A₃∩ … ∩A_n) = P(A₁) P(A₂)..… P(A_n).

Probability of at least one of the n independent events:
If p₁, p₂ ……… p_n be the probabilities of happening of n independent events A₁, A₂ ……… A_n respectively, then

Total probability and Baye’s rule

(1) The law of total probability:
Let S be the sample space and let E₁, E₂ ……… E_n be n mutually exclusive and exhaustive events associated with a random experiment. If A is any event which occurs with E₁ or E₂ or …or E_n, then
P(A) = P(E₁) P(A/E₁) + P(E₂) P(A/E₂) + ….. P(E_n)P(A/E_n).

(2) Baye’s rule:
Let S be a sample space and E₁, E₂ ……… E_n be n mutually exclusive events such that

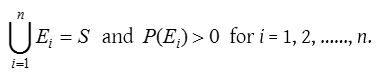
We can think of E_i’s as the causes that lead to the outcome of an experiment. The probabilities P(E_i), i = 1, 2, ….., n are called  prior probabilities. Suppose the experiment results in an outcome of event A, where P(A) > 0. We have to find the probability that the observed event A was due to cause E_i, that is, we seek the conditional probability P(E_i/A). These probabilities are called posterior probabilities, given by Baye’s rule as

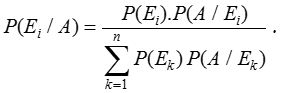
The post What are Addition and Multiplication Theorems on Probability? appeared first on A Plus Topper.

from A Plus Topper
via Learning Made Simple 360

*Note that these contents are Autoblogged from A Plus Topper and cannot be edited.