What is the Multinomial Theorem?

What is the Multinomial Theorem?

Multinomial theorem

Let x₁, x₂, …….., x_m be integers. Then number of solutions to the equation x₁ + x₂ +…….. + x_m = n  …..(i)
Subject to the condition
a₁ ≤ x₁ ≤ b₁, a₂ ≤ x₂ ≤ b₂, ……, a_m ≤ x_m ≤ b_m  …..(ii)
is equal to the coefficient of xⁿ in

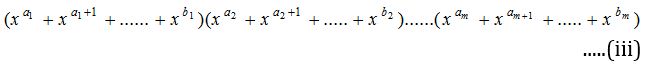
This is because the number of ways, in which sum of m integers in (i) equals n, is the same as the number of times xⁿ comes in (iii).

(1) Use of solution of linear equation and coefficient of a power in expansions to find the number of ways of distribution : (i) The number of integral solutions of x₁ + x₂ + x₃ +…….. + x_r = n where x₁ ≥ 0, x₂ ≥ 0, …….., x_r ≥ 0 is the same as the number of ways to distribute n identical things among r persons.
This is also equal to the coefficient of xⁿ in the expansion of (x⁰ + x¹ + x² + x³ + ……)^r

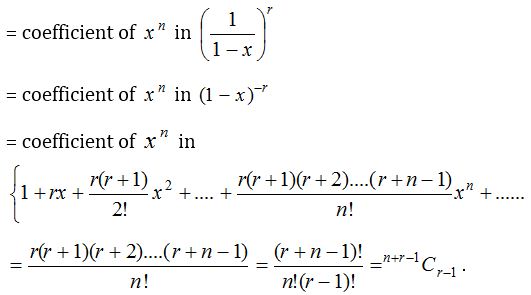
(2) The number of integral solutions of x₁ + x₂ + x₃ +…….. + x_r = n where x₁ ≥ 1, x₂ ≥ 1, …….., x_r ≥ 1 is same as the number of ways to distribute n identical things among r persons each getting at least 1. This also equal to the coefficient of xⁿ in the expansion of (x⁰ + x¹ + x² + x³ + ……)^r.

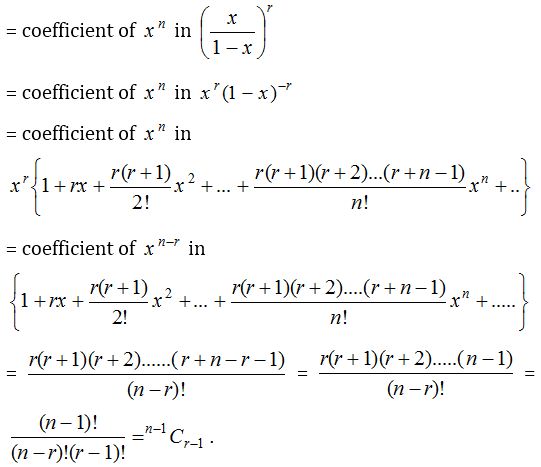
Number of divisors

(5) The number of ways in which N can be resolved as a product of two factors is

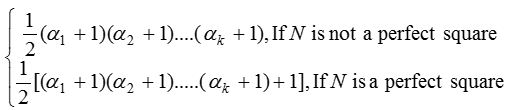
(6) The number of ways in which a composite number N can be resolved into two factors which are relatively prime (or co-prime) to each other is equal to 2ⁿ⁻¹ where n is the number of different factors in N.

The post What is the Multinomial Theorem? appeared first on A Plus Topper.

*Note that these contents are Autoblogged from A Plus Topper and cannot be edited.