Integration Rules and Formulas

Integration Rules and Formulas

Integral of a Function

A function ϕ(x) is called a primitive or an antiderivative of a function f(x), if ?'(x) = f(x).
Let f(x) be a function. Then the collection of all its primitives is called the indefinite integral of f(x) and is denoted by ∫f(x) dx.
Thus,

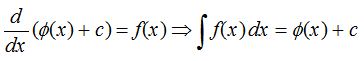
where ϕ(x) is primitive of f(x) and c is an arbitrary constant known as the constant of integration.

Integration Rules

1. Chain rule :
   ∫u.v dx = uv₁ – u’v₂ + u”v₃ – u”’v₄ + ……… + (–1)^n­–1 u^n–1v_n + (–1)ⁿ ∫uⁿ.v_n dx
   Where  stands for n^th differential coefficient of u and stands for n^th integral of v.
2. Sum Rule
   ∫(f + g) dx = ∫f dx + ∫g dx
3. Difference Rule
   ∫(f – g) dx = ∫f dx – ∫g dx
4. Multiplication by constant
   ∫cf(x) dx = c∫f(x) dx
5. Power Rule (n≠-1)
   ∫xⁿ dx = xⁿ⁺¹/(n+1) + C

Fundamental Integration Formulae

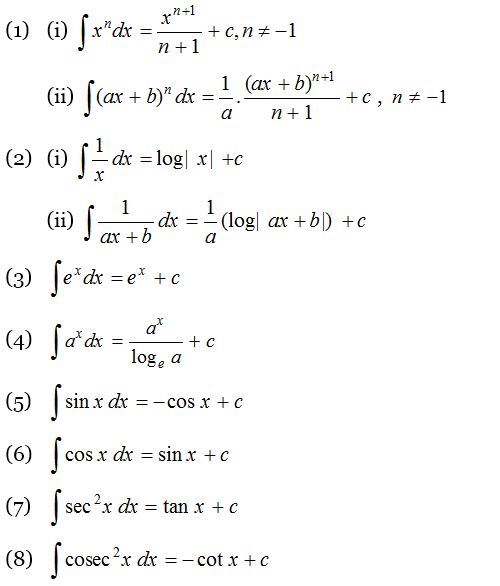
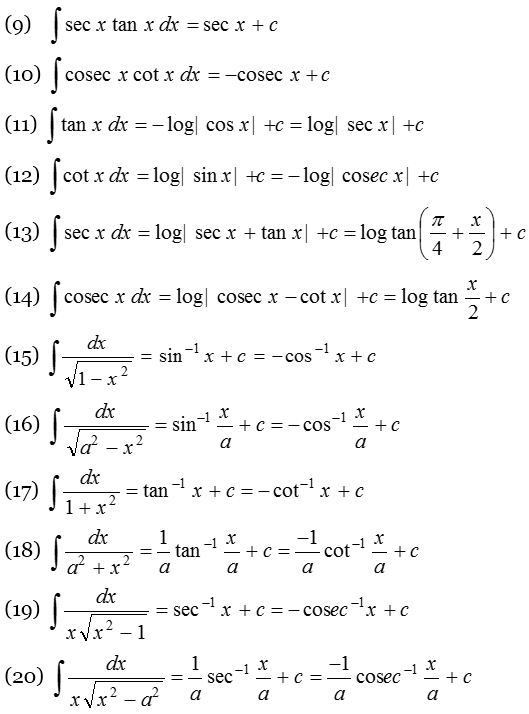
In any of the fundamental integration formulae, if x is replaced by ax+b, then the same formulae is applicable but we must divide by coefficient of x or derivative of (ax+b) i.e., a. In general, if ∫f(x) dx = ϕ(x) + c, then

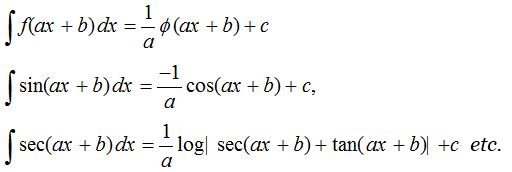
Some more Results

The post Integration Rules and Formulas appeared first on A Plus Topper.

*Note that these contents are Autoblogged from A Plus Topper and cannot be edited.