What is Logarithmic Series Expansion ?

What is Logarithmic Series Expansion ?

Logarithmic Series

Definition

An expansion for log_e (1 + x) as a series of powers of x which is valid only, when |x|<1.

Expansion of logarithmic series

Expansion of log_e (1 + x) if |x|<1 then

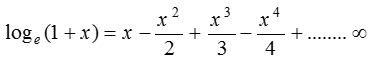
Replacing x by −x in the logarithmic series, we get

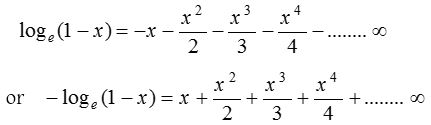
Some Important results from logarithmic series

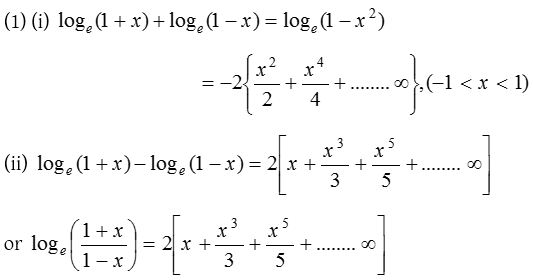
(2) The series expansion of log_e (1 + x) may fail to be valid, if |x| is not less than 1. It can be proved that the logarithmic series is valid for x = 1. Putting x = 1 in the logarithmic series.
We get,

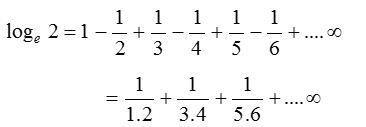
(3) When x = −1, the logarithmic series does not have a sum. This is in conformity with the fact that log(1 – 1) is not a finite quantity.

Difference between the exponential and logarithmic series

(2) In the exponential series the denominator of the terms involve factorial of natural numbers. But in the logarithmic series the terms do not contain factorials.
(3) The exponential series is valid for all the values of x. The logarithmic series is valid, when |x|< 1.

The post What is Logarithmic Series Expansion ? appeared first on A Plus Topper.

*Note that these contents are Autoblogged from A Plus Topper and cannot be edited.